Yksikkövektorimerkinnät | Vektorit ja välilyönnit Lineaarinen algebra | Khan-akatemia
Kun he selittävät ulottuvuutta W, se esitetään X-akselin negatiivisena puolena. Miksi ulottuvuus W on negatiivinen X? Eikö se todellakaan ole oma ulottuvuus?

- Yritä piirtää 4-ulotteinen kaavio 2-ulotteiselle pinnalle. Tämän he keksivät (sinun oikeutesi, vaikka se ei ole loistava kaavio).
Kuten @NendoTaka on maininnut, on melko vaikea piirtää 4d-objekti 2d-pinnalle.
Näin ulottuvuus toimii:
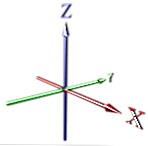
yhdellä ulottuvuudella piste lähetetään loputtomasti, jolloin muodostuu viiva (katso X)
2d: ssä lisätään siihen kohtisuora ulottuvuus (katso X, Y).
Sitten menemme taas kohtisuoraan ja laajennamme ylöspäin saadaksemme kolmannen ulottuvuuden (katso X, Y, Z).
Koska 3d> 2d, emme voi edustaa sitä hyvin paperilla taittamatta paperia tai lisäämättä lisää arkkia sen päälle - kaikki ovat todella epäkäytännöllisiä näytöllä katselemiseksi. Joten sen sijaan käytämme perspektiiviä - miten silmämme havaitsevat 3d: n. Yleensä kulmat ovat ~ 30 astetta.

Ja se näyttää melko hyvältä, koska silmämme eivät näe tässä perinteisessä kolmiulotteisessa mielessä, joten matkivat niin. Mutta kun haluamme edustaa 4. ulottuvuutta, meillä ei ole mihin verrata sitä. Meidän on mentävä jälleen kohtisuoraan, ja tämä on silmiemme vaikea ymmärtää, koska meillä ei ole paljon viitteitä.
Tässä on esimerkki neljännen ulottuvuuden kuvauksesta:
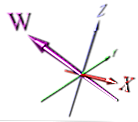
Tämä on oikeampi tapa näyttää ulottuvuus, mutta se perustuu silti perspektiiviin - eikä myöskään ole heti selvää, että se on uusi ulottuvuus ensi silmäyksellä.
Animaattorit päättivät luultavasti tehdä jotain yksinkertaista, joka olisi helpompi animoida. Vaikka kiertäessäsi yllä olevaa kuvaa, X- ja W-mitat voivat olla päällekkäisiä - eikä tämä olisi ilmeistä kuvassa ilman nuolinäppäimiä.
Joten joo, he ovat väärässä - mutta ei ole myöskään yksinkertaista tapaa edustaa 4 ulottuvuutta yhdellä paperiarkilla
Koordinoi kuvalähteet ja hyvä lukutaito
3- 1 Ollakseni oikeudenmukainen, on olemassa monia tavanomaisia tapoja heijastaa 4-ulotteisia esineitä, kuten tesserakteja ja 3-palloja, kolmeen ulottuvuuteen (ja sitten kahteen ulottuvuuteen tavallisilla tavoilla), jotka ovat huomattavasti parempia kuin esityksessä käytetty, monet joista on lisäbonuksena näyttää viileämmältä kuin näyttelyssä käytetty.
- @senshin Voi varmasti, mutta luulen, että animaattorit halusivat myös selittää jotain ällistyttävän
- 1 Voit käyttää muita asioita kuin sijaintia osoittamaan kuinka pitkälle akselilla jokin on, kuten väri.